алгебра логики

КОНСПЕКТ УРОКОВ В 11 КЛАССЕ

ТЕМА: ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ

Ответы на контрольные вопросы

1. что изучает алгебра логики? 

высказывания

2. какими элементарными объектами оперирует алгебра логики? 

изучает логические высказывания и способы установления их истинности

3. какие значения принимают объекты алгебры логики

истина или ложь

4. какая из приведенных фраз является высказыванием и имеет значение "истина"

"человеку свойственно ошибаться"

"В России существует закон об обязательном среднем образовании"

5. Какие из приведенных фраз не являются высказываниями?

"АБС<>ВСА"

"Все на борьбу с бездорожьем!"

7. Как образуются сложные высказывания?

Сложное высказывание образуется из простых с помощью логических операций

8. Какая из предложенных фраз является результатом конъюнкции простых высказываний?

в) корреспондент должен быть эрудированным и коммуникабельным

10) что отображает таблица истинности?

значение логической функции для разных сочетаний аргументов

12. В каком случае можно утверждать, что высказывания равносильны?

если эти высказывания равны на множестве значений всех простых высказываний, входящих в них

(или если у них идентичны таблицы истинности)

13. какие существуют способы установления равносильности высказываний?

при помощи сравнения таблиц истинности

путем приведения одного высказывания к другому

путем приведения обоих высказываний к одному выражению

Тема: Логические операции "Импликация", "Эквивалентность"

Логическое следование или импликация:

Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.

Таблица истинности для импликации

 

A	B	F
1	1	1
1	0	0
0	1	1
0	0	1

 

импликацию можно выразить через основные логические операции: A→B=¬AVB=¬(АΛ¬В);

 

 Логическая равнозначность или эквивалентность:

Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.

Таблица истинности для эквивалентности

 

A	B	F
1	1	1
1	0	0
0	1	0
0	0	1

Порядок выполнения логических операций в сложном логическом выражении

1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.

Пример:

AV¬BΛC→D↔E.

Порядок выполнения:

1. ¬B
2. (¬B)ΛC
3. AV((¬B)ΛC)
4. (AV((¬B)ΛC))→D
5. ((AV((¬B)ΛC))→D)↔E

Для изменения указанного порядка выполнения логических операций используются скобки.

Логическая операция/ соответствие в русском языке	Обозначение	Диаграмма Эйлера-Венна	Таблица  истинности
инверсия (отрицание, логическое "НЕ")/ "...не...", "неверно, что..."	¬		A	¬A
			0	1
			1	0
конъюнкция (логическое "И")/ "...и..."	Λ, &		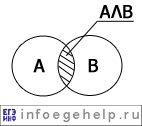A	B	AΛB
			0	0	0
			0	1	0
			1	0	0
			1	1	1
дизъюнкция (логическое "ИЛИ") "...или...", "...либо..."	V		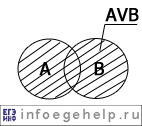A	B	AVB
			0	0	0
			0	1	1
			1	0	1
			1	1	1
импликация (следование)/ "если...,то...", "когда..., тогда..."	→		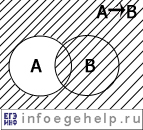A	B	A→B
			0	0	1
			0	1	1
			1	0	0
			1	1	1
эквивалентность (тождество) "тогда и только тогда, когда"	↔, ≡		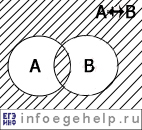A	B	A↔B
			0	0	1
			0	1	0
			1	0	0
			1	1	1

Пример выполнения операций с двоичными числами 

Задание:

1. Рассмотреть пример 3.5 на стр 124
2. Выполнить задания: 3.19, 3.20, 3.21, 3.22
3. Выполнить задания 3.28, 3.29, 3.32, 3.33

Тема: Логические выражения, соответствующие таблице истинности. Графический метод алгебры логики

План урока:

записать новые комбинации клавиш для управления Windows - окнами

1)Window +D

2)Alt+Tab, Windows+Shift+Tab

3)Alt+SpaceBar

4)Ctrl+F4

5)Alt+F4

6)Windows+—>(<—)

7)Shift+F12

8)Ctrl+N

9)Ctrl+O

10)Alt+PrintScreen

1) ответить на контрольные вопросы стр 134

2) выполнить задание 3.39 стр 134

3) выполнить задание 3.42 стр 135

4) выполнить задания на сайте:

а)  http://learningapps.org/405002

б) http://learningapps.org/275914

в) http://learningapps.org/262676

д/з ответить на контрольные вопросы после §3.4 стр 142

РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ

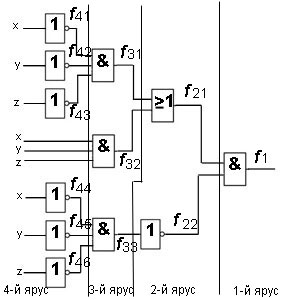
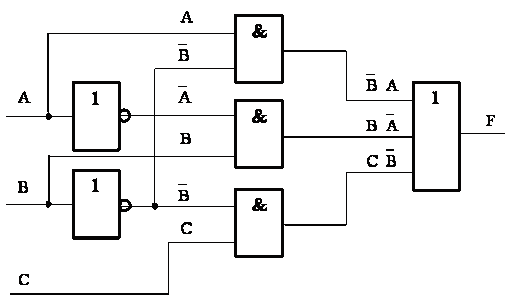
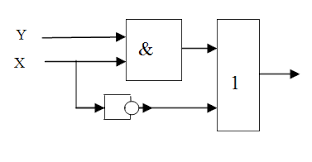
ЛОГИЧЕСКИЕ СХЕМЫ

Что выдаст функция на выходе?

---

Графический метод решения логических задач

 

ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ

ПРОЙТИ ТЕСТ НА ЗНАНИЕ СОЧЕТАНИЙ КЛАВИШ ПО РАБОТЕ С WINDOWS - ОКНАМИ

СМОТРИМ ПРЕЗЕНТАЦИЮ "ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ"

1. ОТВЕТИТЬ НА КОНТРОЛЬНЫЕ ВОПРОСЫ СТР 142

2. РЕШИТЬ ЗАДАЧУ 3.44

3. РЕШИТЬ ЗАДАЧУ 3.48

4. ОТВЕТИТЬ НА КОНТРОЛЬНЫЕ ВОПРОСЫ СТР 147

5. РЕШИТЬ ЗАДАЧУ 3,54

Д/З: ПОВТОРИТЬ АЛГЕБРУ ЛОГИКИ, ПОДГОТОВИТЬСЯ К КОНТРОЛЬНОЙ РАБОТЕ (http://www.matburo.ru/ex_dm.php?p1=dmlogika) (http://potehechas.ru/zadachi/zadachi_8.shtml)

Материал для подготовки к контрольной работе